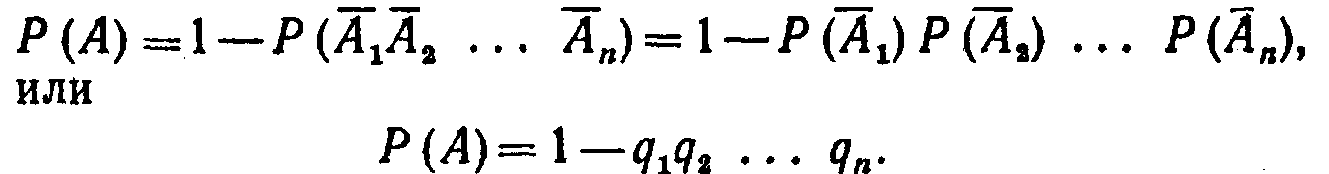Вероятность попадания хотя бы одного

Редактирование задачи
Для ряда задач оказывается удобным использовать геометрическое определение вероятности , которое связывает понятие вероятности с определенной плоской областью. Отметим, что события А 1 и А 2 несовместны тогда и только тогда, когда области g 1 и g 2 не пересекаются. Введенная таким образом вероятность удовлетворяет всем аксиомам вероятности:.





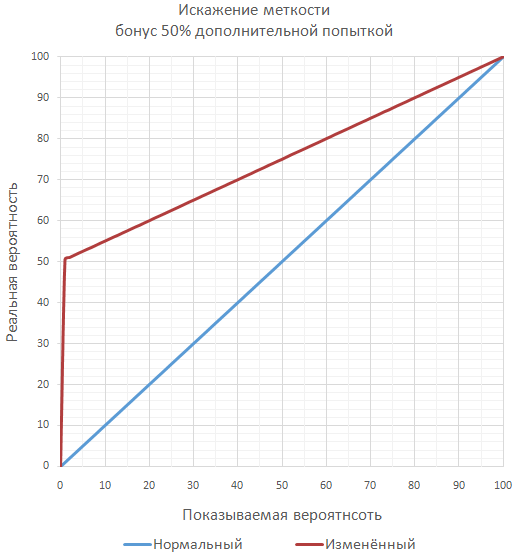
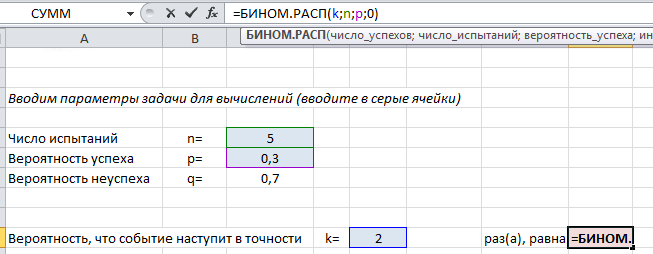
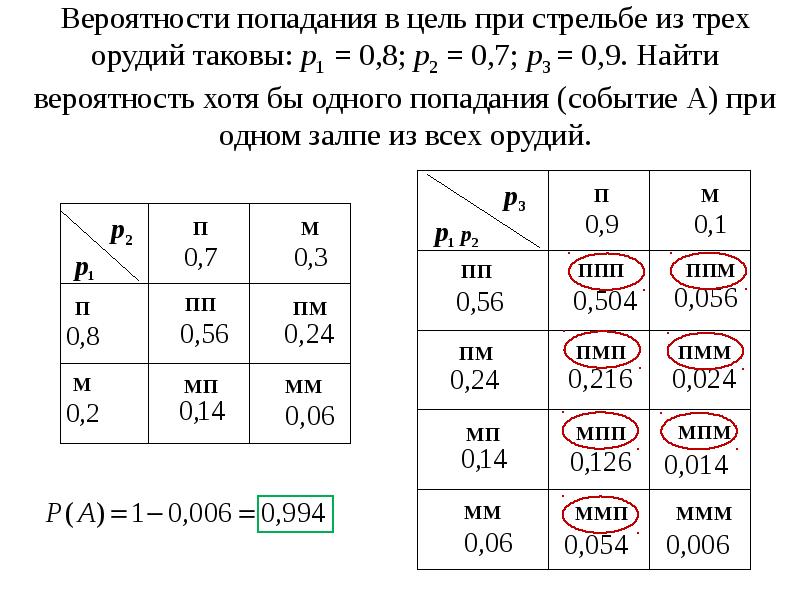
Пусть производится n независимых друг от друга испытаний, в каждом из которых случайное событие А может либо произойти, либо не произойти. Вероятность того, что событие А состоится в каждом испытании одна и та же и равна p. Следовательно, вероятность того, что событие А не произойдет, равна 1— р. Зададимся вопросом, какова будет вероятность того, что при n испытаниях событие А наступит в k из них и, соответственно, в n - k испытаниях не наступит? Для подсчета вероятности пронумеруем испытания. Для начала найдем вероятность наступления события А в испытаниях с определенными k номерами, и ненаступления в остальных n - k испытаниях.

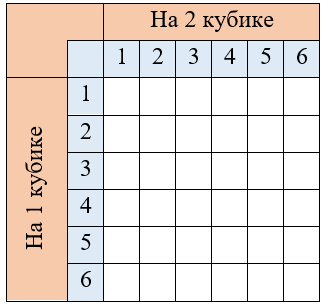





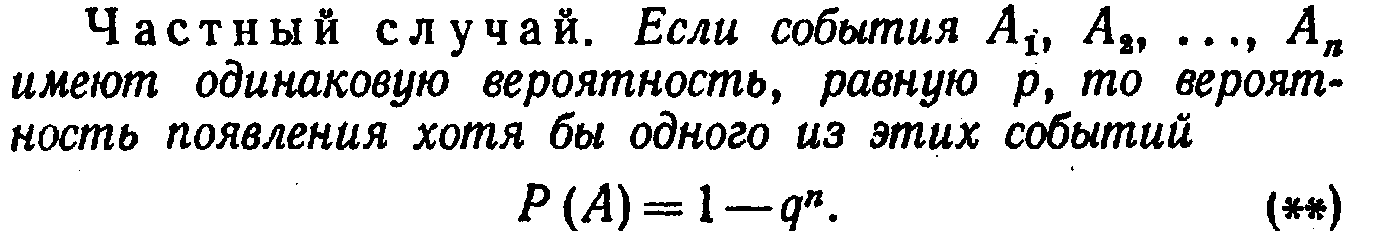


Давайте посчитаем вероятность выпадения орла при броске монеты. Назовем событие выпадения орла событием А. Тогда вероятность события А — это Р А. Как мы и сказали, благоприятным действием является выпадение орла. Такой исход всего один.