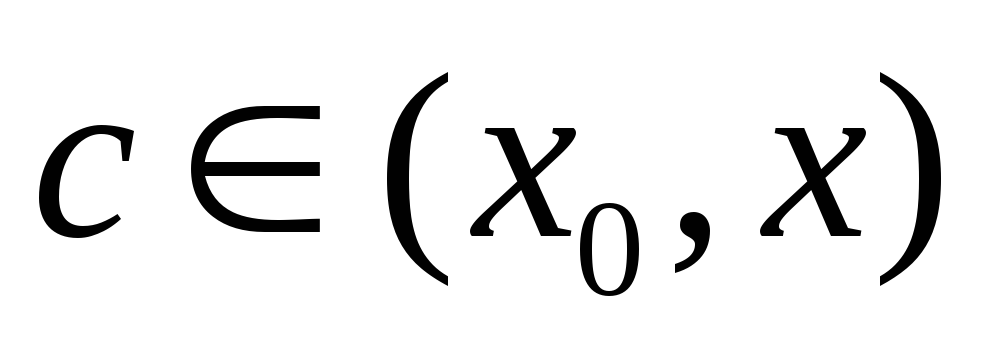Остаточный член в форме

Остаточный член равен разности между заданной функцией и функцией, её аппроксимирующей, тем самым его оценка является оценкой точности рассматриваемой аппроксимации. К указанным формулам относятся формулы типа формулы Тейлора , интерполяционные формулы, асимптотические формулы, формулы для приближённого вычисления тех или иных величин. Так, в формуле Тейлора. При асимптотическом разложении функции.

1.5.14.6. Формула Тейлора с остаточным членом в общей форме (в форме Шлемильха-Роша)

Последний раз редактировалось yoloven Добрый вечер. У меня возникла проблема при оценке количества элементов, которые необходимо взять, чтобы достичь требуемой погрешности. Например, берем функцию. Нужно определить до какого элемента достаточно разложить данную функцию в ряд Тейлора, чтобы погрешность вычислений была меньше, чем. Беру остаточный член в форме Лагранжа Предположим, что ищем погрешность в окрестности точки и тогда должно получаться такое неравенство: Преобразуем немного и получим И что дальше?

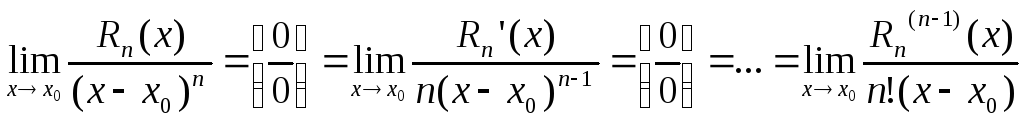
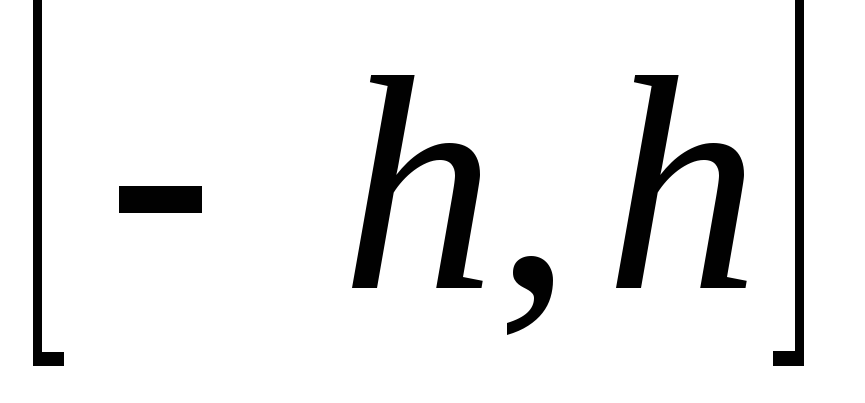
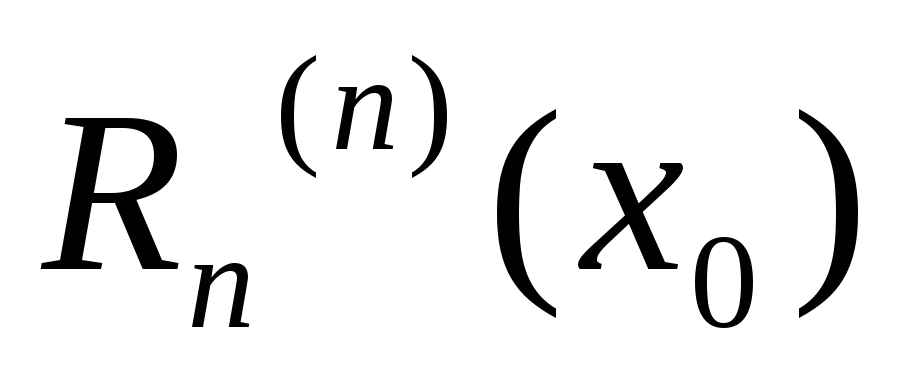
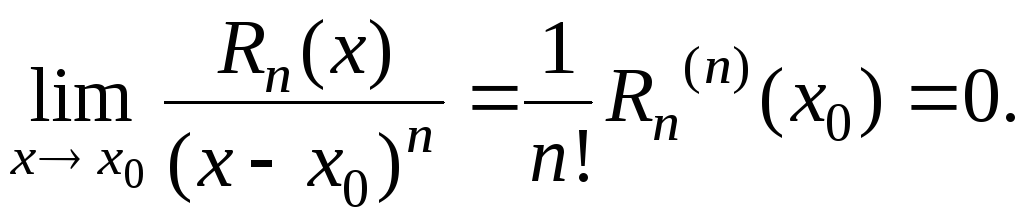
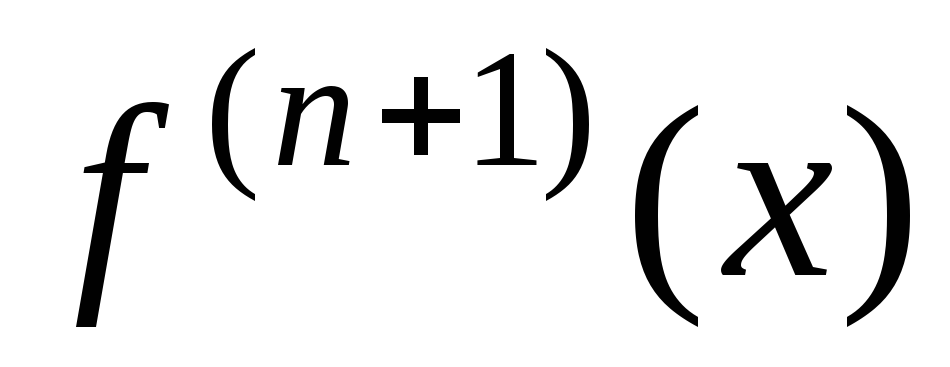
Регистрация Вход. Ольга Александровна, помогите решить! Сколько не мучил эти примерчики толкового ничего не получилось. Подскажите, пожалуйста. Просто у меня некоторые непонятки с формулой остаточного члена в форме Лагранжа для этой функции возникли.

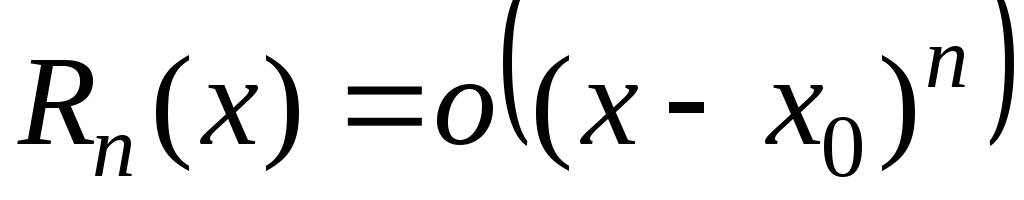
Ост а точный чл е н приближённой формулы, разность между точным и приближённым значениями представляемого этой формулой выражения. В зависимости от характера приближённой формулы О. Обычно задача исследования О. Например, приближённой формуле. Далее, О.

Похожие статьи

• Ножки в чулках ласкают член
• Длина полового члена порно звезд
• Майл смотреть порно безплатно без регистрации большой член
• Смотреть порно скачет жопой на огромном члене